Skip to main content

Animation

In this section we will learn step by step how to run (and port possibly) and optimize animation code from Wolfram Mathematica to WLJS.

An example by Peter Tenisheff (tenishefff@yandex.ru)

Here is an original Wolfram Mathematica code of a triple pendulum:

Initialization of variables, equations

Details

Optimization​

Step 0​

Let's run Mathematica's code for animation directly:

Animate[
    Graphics[
      {
        Thick, Black,
        Line[{{0, 0}, {xC[t, 1], yC[t, 1]}, {xC[t, 2], yC[t, 2]}, {xC[t, 3], yC[t, 3]}}],
        
        Blue, PointSize[0.03], Point[{xC[t, 1], yC[t, 1]}],
        Red, PointSize[0.03], Point[{xC[t, 2], yC[t, 2]}],
        Black, PointSize[0.04], Point[{xC[t, 3], yC[t, 3]}],
        
        {Green, Opacity[0.5], Line[trajectory[[;; Floor[t/0.05] + 1]]]}
      },
      PlotRange -> {{-3.5, 3.5}, {-3.5, 0.5}},
      Axes -> True,
      Background -> White,
      ImageSize -> 500
    ],
    {t, 0, timeMax, 0.05},
    AnimationRate -> 5
]

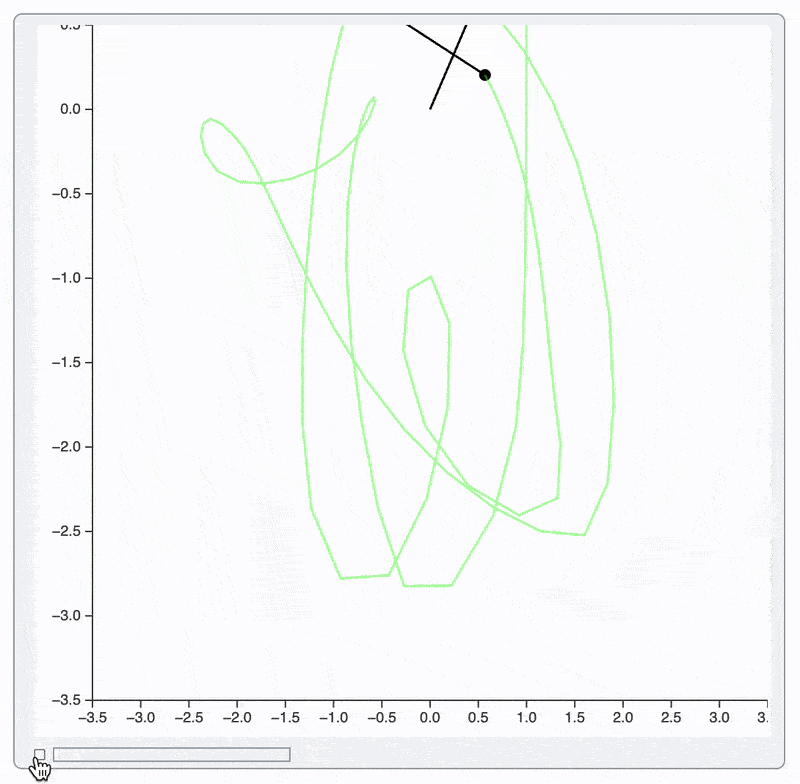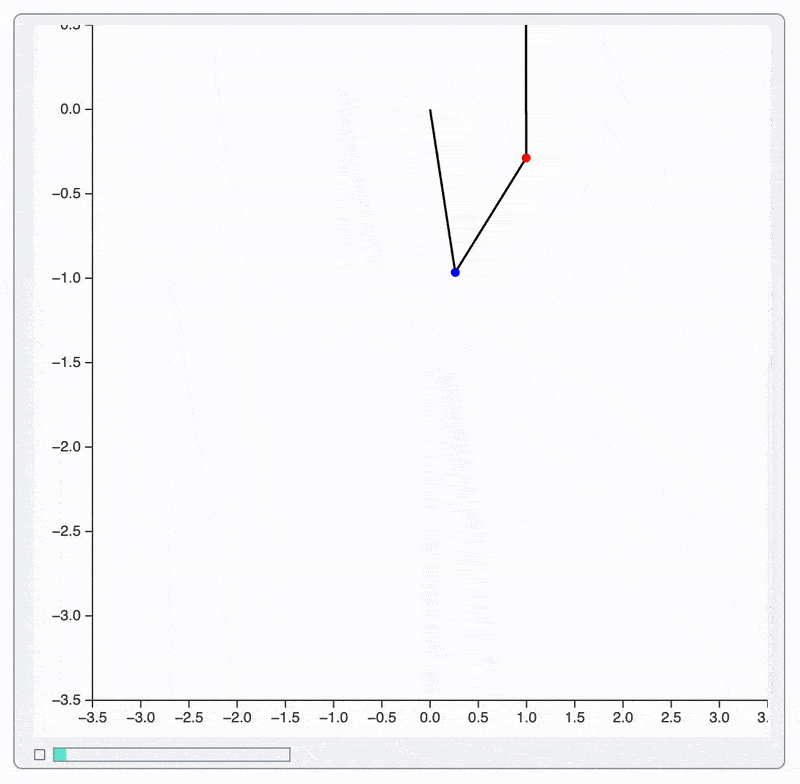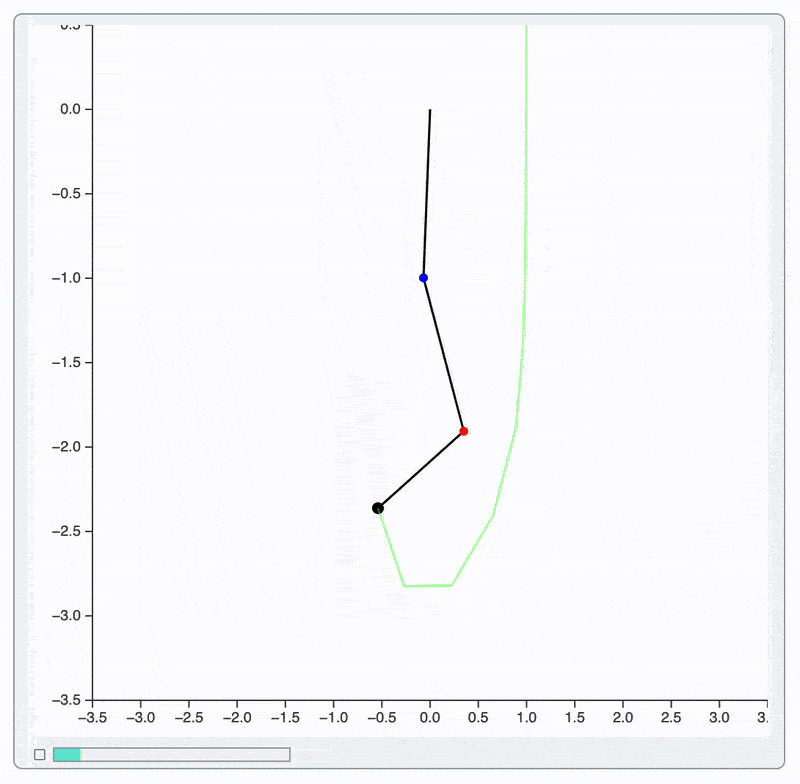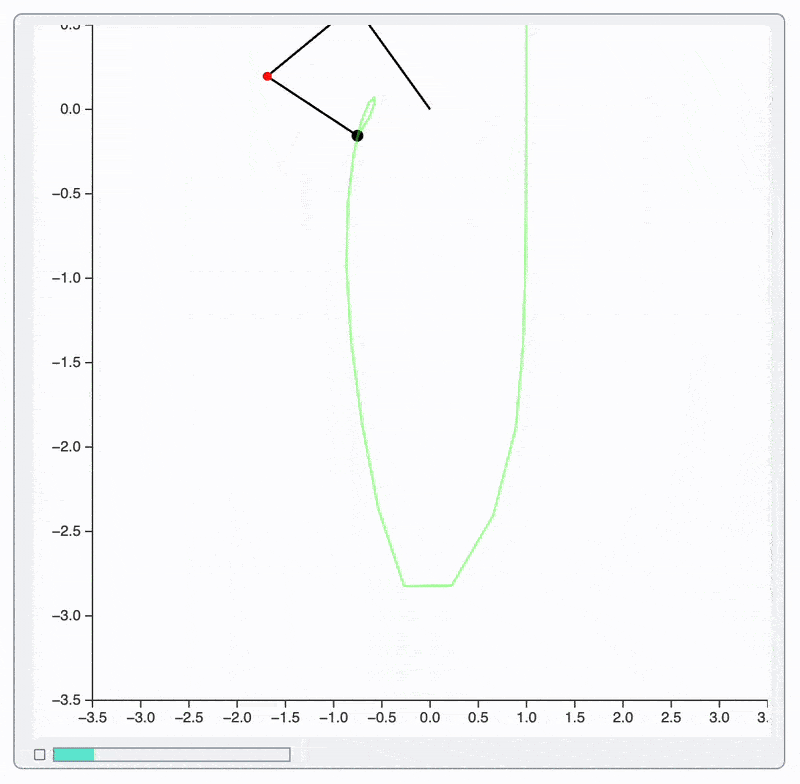
It is slow and shakes, but it works. Here is why:

  • each frame a new Graphics object is created and copied to the frontend and then evaluated ❌
  • each frame creates a new instanced and destroys an old one ❌

This is a huge waste of resources considering that we only need to change a few points and line segments.

Step 1​

As a first step we find what primitives we need to change each frame:

  • Point x3
  • Line x2 (one for pendulum segments and one for trajectory)

Then we can image:

{
	...,
	Red, Point[pt1 // Offload],
	Blue, Point[pt2 // Offload], 
	...
}

or even better - reduce the number of symbols used:

{
	...,
	Line[{{0,0}, pts[[1]], pts[[2]], pts[[3]]} // Offload],
	Red, Point[pts[[1]] // Offload],
	Blue, Point[pts[[2]] // Offload], 
	...
}

To prevent Animate from reevaluation of the whole Graphics expression we provide a custom "UpdateFunction", which overrides the default behavior and update only our pts symbol:

Module[{pts, track},
  Animate[
    Graphics[
      {
        Thick, Black,
        Line[{{0,0}, pts[[1]], pts[[2]], pts[[3]]} // Offload],
        
        Blue, PointSize[0.03], Point[pts[[1]] // Offload],
        Red, PointSize[0.03], Point[pts[[2]] // Offload],
        Black, PointSize[0.04], Point[pts[[3]] // Offload],
        
        {Green, Opacity[0.5], Line[track // Offload]}
      },
      PlotRange -> {{-3.5, 3.5}, {-3.5, 0.5}},
      Axes -> True,
      Background -> White,
      ImageSize -> 500
    ],
    {t, 0, timeMax, 0.05},
    "UpdateFunction" -> Function[t,
      track = trajectory[[;; Floor[t/0.05] + 1]];
      pts = Table[{xC[t, i], yC[t, i]}, {i,3}];
      False
    ],
    AnimationRate -> 30
  ]
]

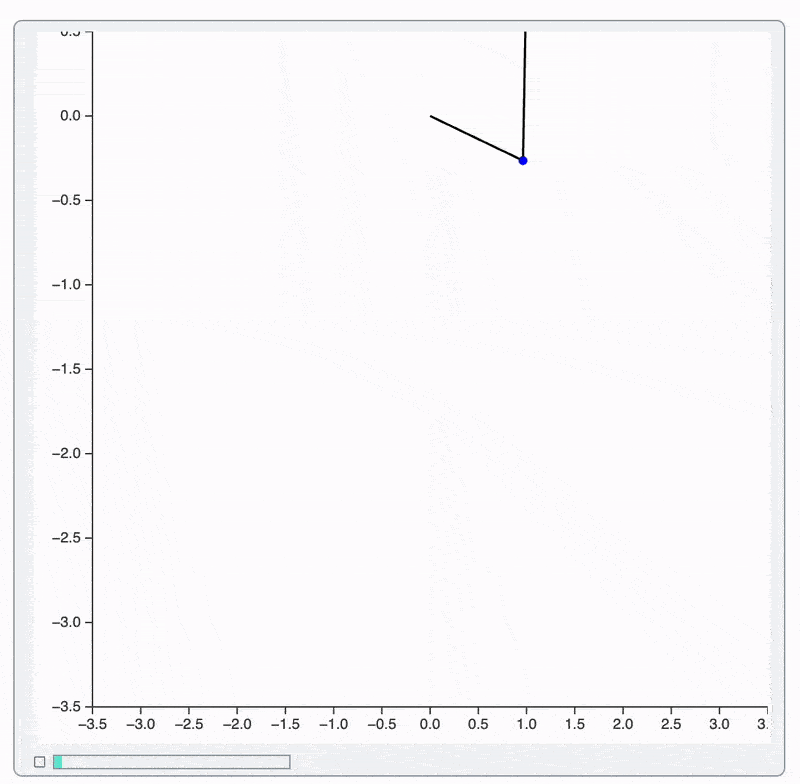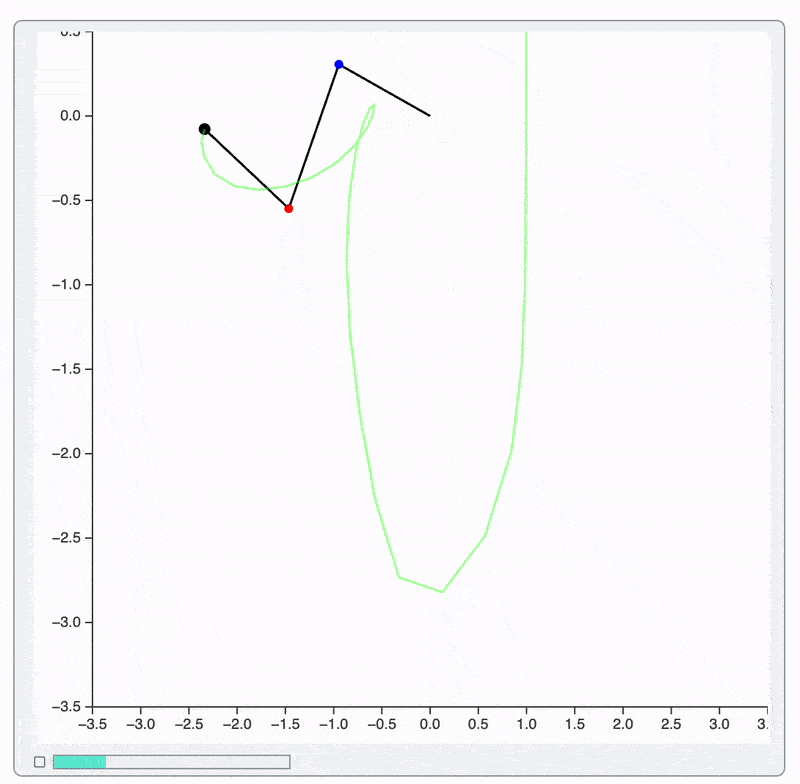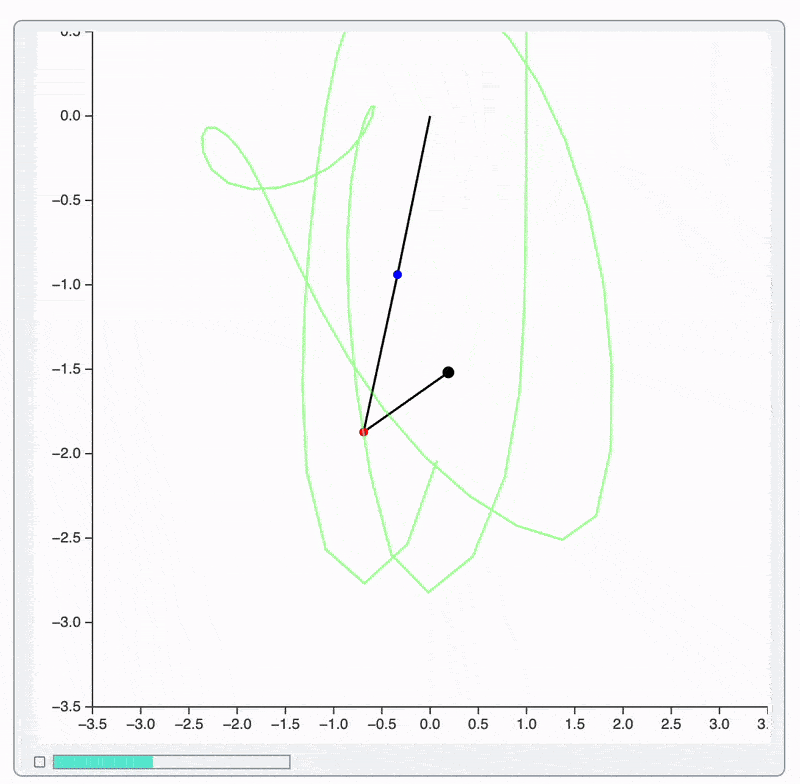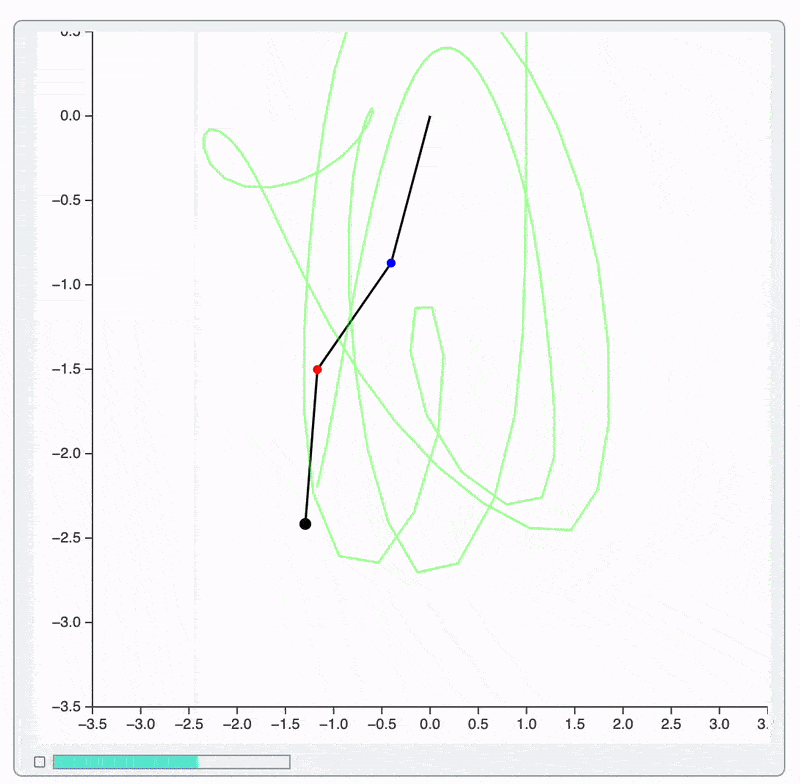
Note, that we also increased a frame rate up-to 30. This works much smoother because:

  • Graphics expression stays and does not change ✅
  • Only Line and Point are updated ✅

Step 3​

You may noticed an odd-looking shaking of a trajectory on the background. It is a side-effect of interpolation enabled by the default on Graphics. It makes all transitions even smoother (60 or 120 FPS), but cannot handle properly Line with variable number of segments.

One can disable the transition animation completely by setting an option:

Graphics[..., TransitionType -> None]

This might give a performance boost in the case of a very fast animations (where the frame rate is close to 30).

Another way is to disable it only for Line primitive using Directive:

Module[{pts, track},
  Animate[
    Graphics[
      {
        Thick, Black,
        Line[{{0,0}, pts[[1]], pts[[2]], pts[[3]]} // Offload],
        
        Blue, PointSize[0.03], Point[pts[[1]] // Offload],
        Red, PointSize[0.03], Point[pts[[2]] // Offload],
        Black, PointSize[0.04], Point[pts[[3]] // Offload],
        
        {Green, Opacity[0.5], Directive[TransitionType->None], 
        Line[track // Offload]}
      },
      PlotRange -> {{-3.5, 3.5}, {-3.5, 0.5}},
      Axes -> True,
      Background -> White,
      ImageSize -> 500
    ],
    {t, 0, timeMax, 0.05},
    "UpdateFunction" -> Function[t,
      track = trajectory[[;; Floor[t/0.05] + 1]];
      pts = Table[{xC[t, i], yC[t, i]}, {i,3}];
      False
    ],
    AnimationRate -> 30
  ]
]

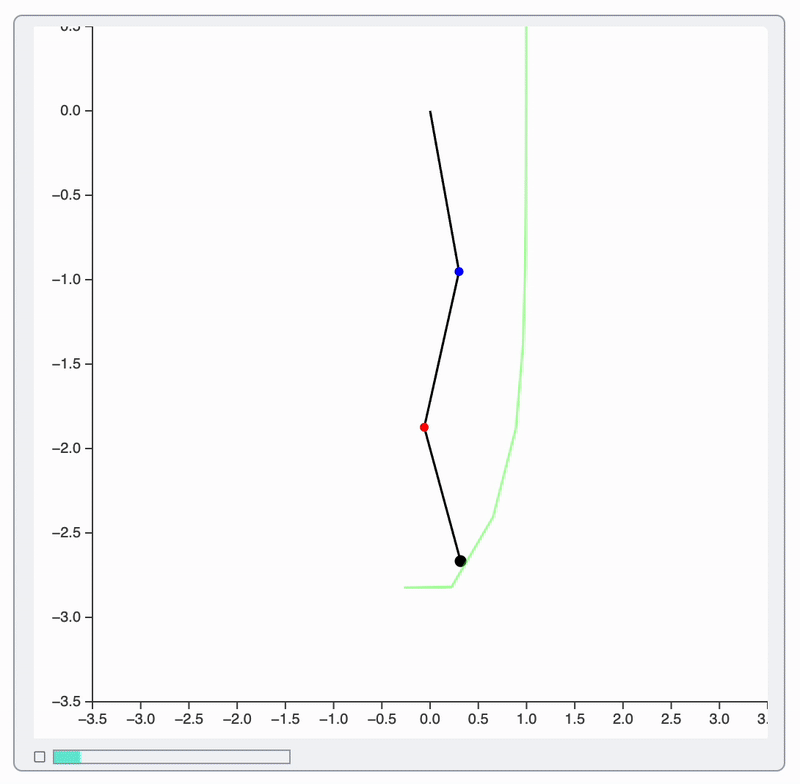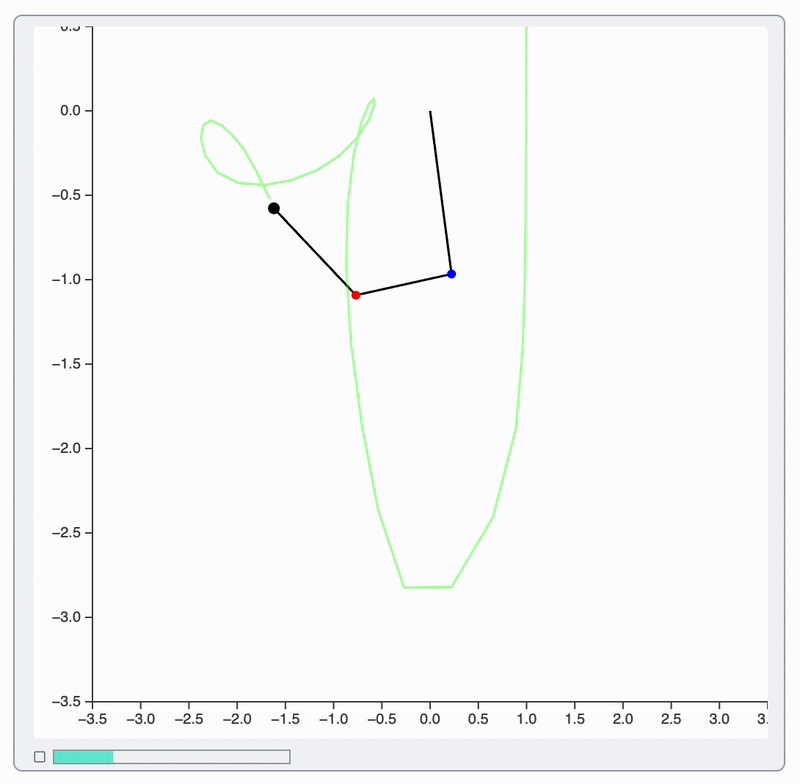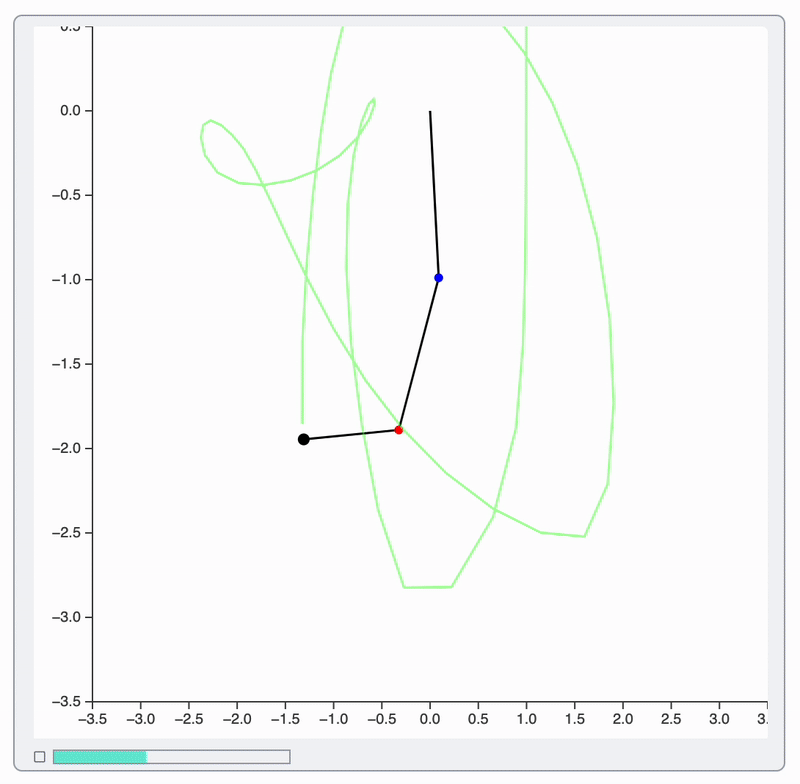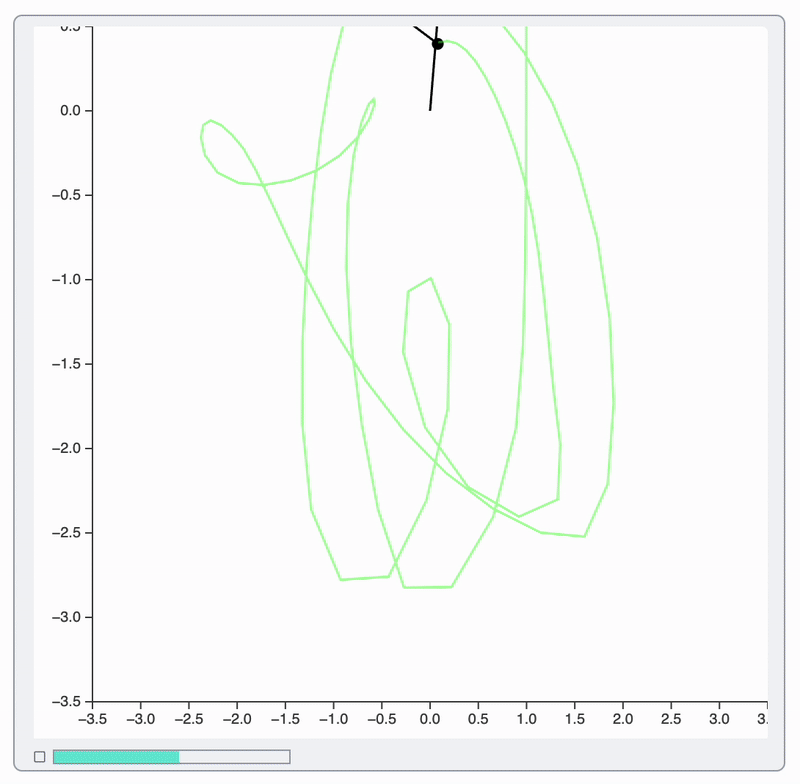
As a result:

  • Points and segments of a pendulum interpolated to get extra frames ✅
  • Background trajectory line is updated as it is ✅
Last updated on