Prototyping

Imagine we want to recreate this background used in a presentation:

At first glance, it looks like a few circles with a large radius, dashed lines, and three Disk elements. Programming this manually would be cumbersome. However, we can create our own tools for this specific task in just a few lines.

Placing Objects

We use the Navigation gizmo to assist in placing straight lines and disks.

Then, select the highlighted regions and run navigation ... from the command palette.

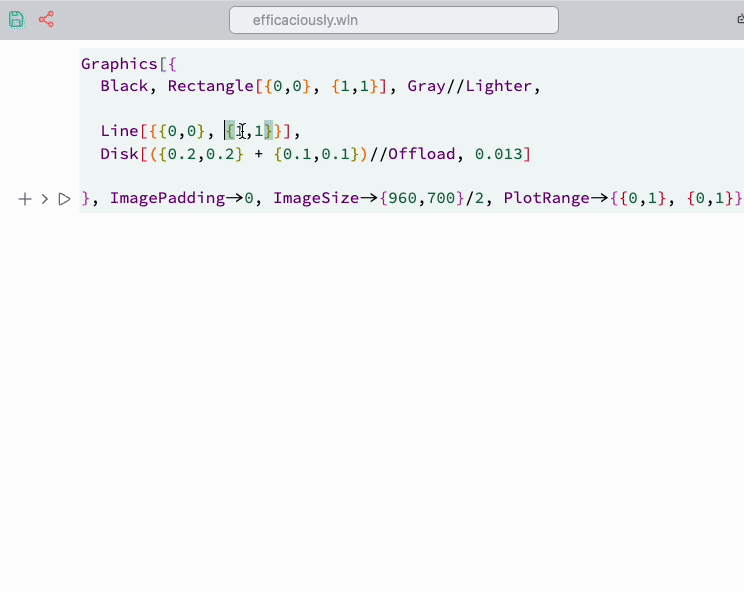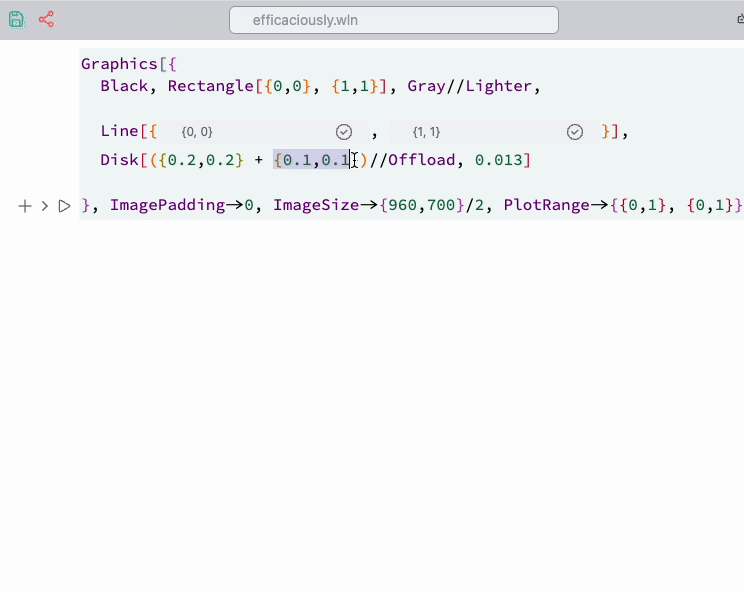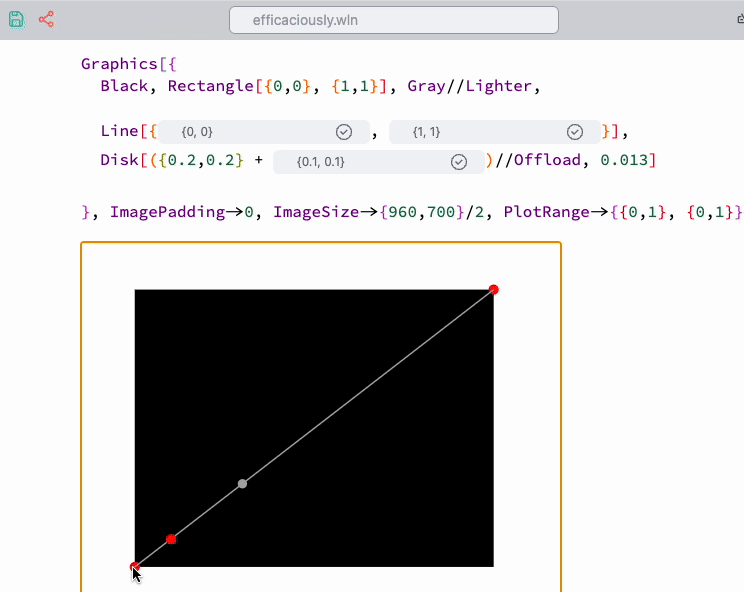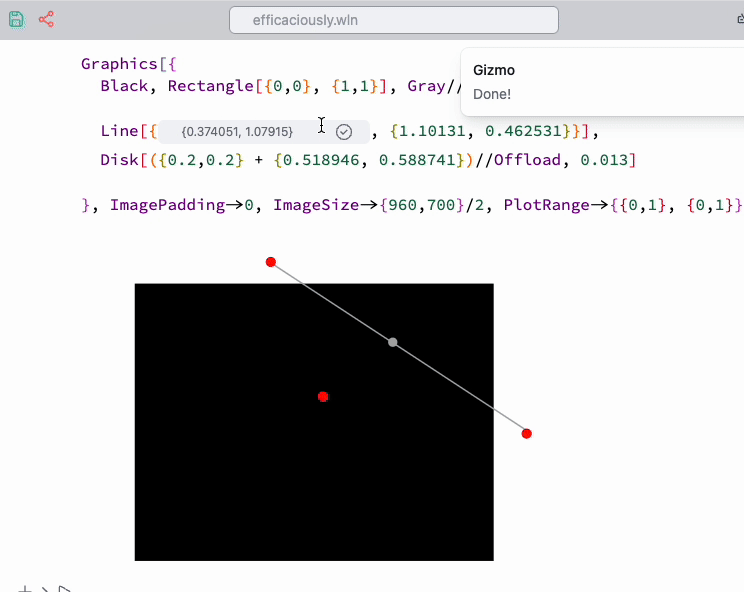
It is better to add offsets to the positions, like we did with Disk:

This prevents the navigation gizmo from overlapping with the actual graphic primitives being positioned.

Parameterized Curves

Let’s examine some curves.

A prototype for circles:

curveGenerator[pt1_, pt2_] := Line[With[{
  radius = pt1,
  pos = pt2
},
  Table[Norm[pos - radius]{Sin[i], Cos[i]} + pos, {i, 0, 2Pi, 0.1}]
] // Offload]

This function produces a circle defined by two points. The key feature is that it accepts any symbol as pt1 / pt2, including dynamic ones. Since all internals of Line, including Table, are wrapped in Offload, the calculation occurs directly on the frontend (WLJS Interpreter), while the Wolfram Kernel only provides values for the control points.

To assist with placement, use the Navigation gizmo snippet from the command palette. It automatically generates a temporary dynamic symbol and a gizmo for it:

Apply it from the command palette to the selection, as shown below:

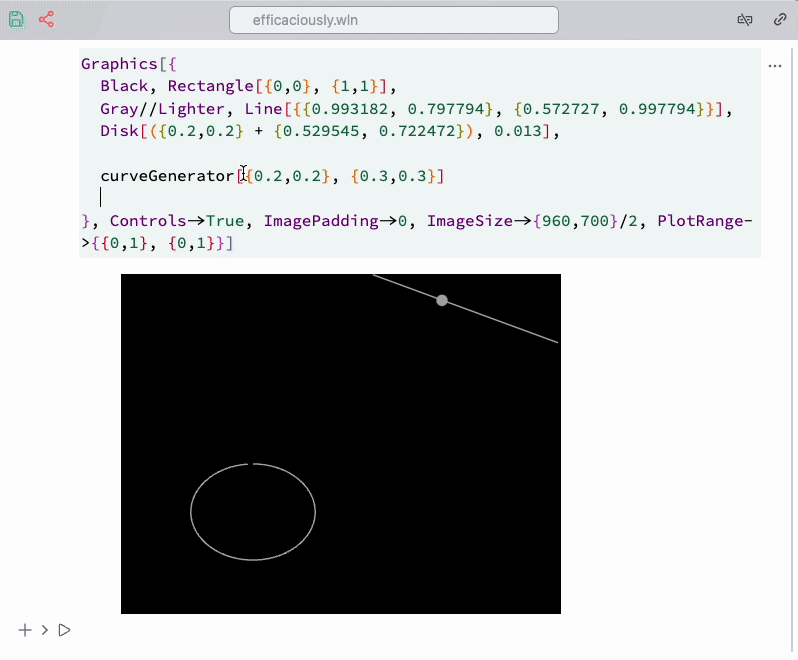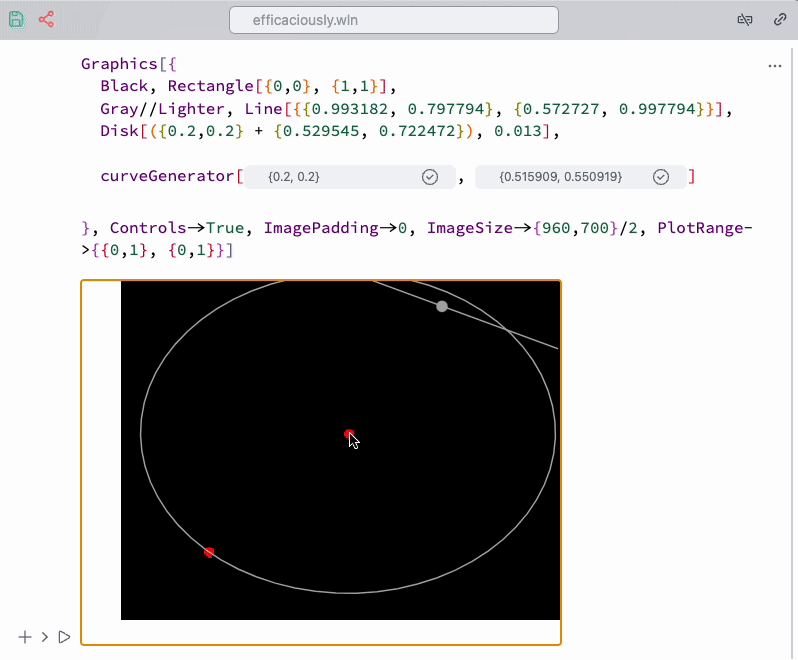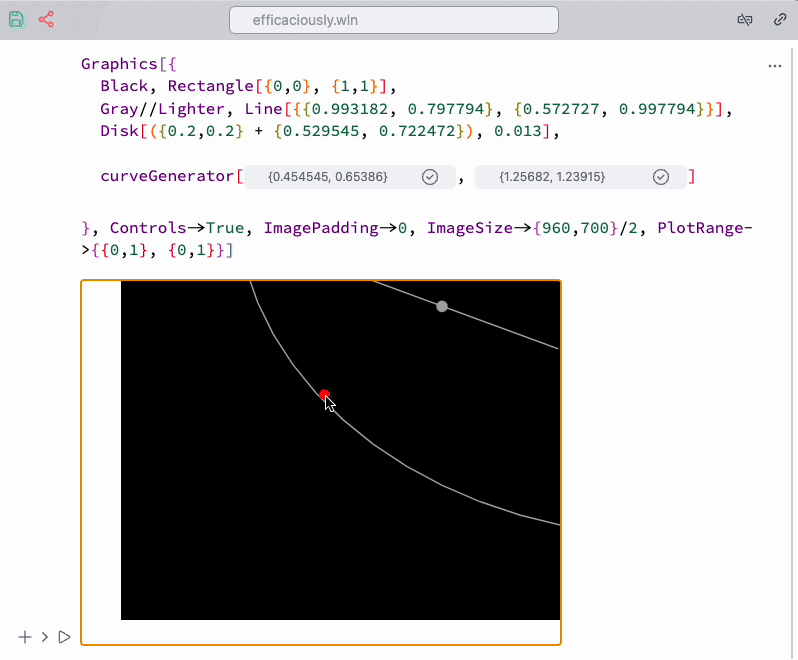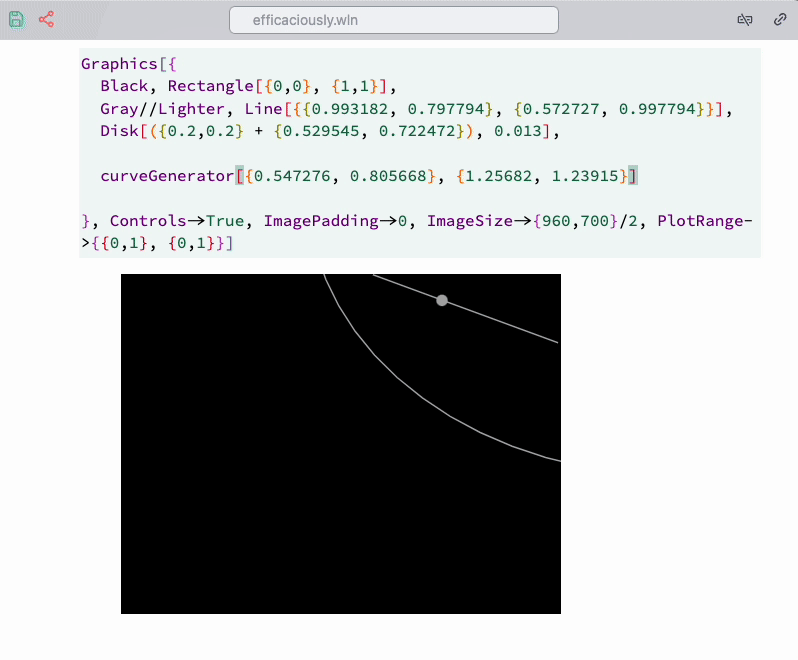
Once we have placed all objects, why not animate them?

Animation

To animate the curves, we need to modify curveGenerator slightly:

ClearAll[curveGenerator];

curveGenerator[radius_, center_, dashed_:False] := With[{
  cell = ResultCell[]
}, LeakyModule[{
  pts = Table[Norm[center - radius] {Sin[i], Cos[i]} +
         center, {i, 0, 2 Pi + 0.1, 0.1}],
  pt = {10,10},
  modulation = 0.,
  phase = 0.,
  task
}, 

  EventHandler[cell, {
    "Destroy" -> Function[Null, Print["Destroy"]; TaskRemove[task]]
  }];

  task = SetInterval[
      pts = Table[(Norm[center - radius] + 0.02 modulation Sin[50. i + 30 phase]) {Sin[i], Cos[i]} +
         center, {i, 0, 2 Pi + 0.1, 0.01}];

         pt = With[{i = 3. phase},(Norm[center - radius] + 0.01 modulation Sin[50. i + 30 phase]) {Sin[i], Cos[i]} +
         center];

      phase = phase + 0.02;
      modulation = Sin[phase/2];
  , 100];  
  
  If[dashed // TrueQ, 
    {SVGAttribute[Line[pts // Offload],"stroke-dasharray"->"10"], Disk[pt // Offload, 0.013]} 
  ,
    {Line[pts // Offload], Disk[pt // Offload, 0.013]} 
  ]
] ]

Now, using SetInterval, the curves animate at 100 ms intervals and remove the task if the output cell is destroyed.

By putting everything together, we achieve a smooth animated title slide for your presentation.

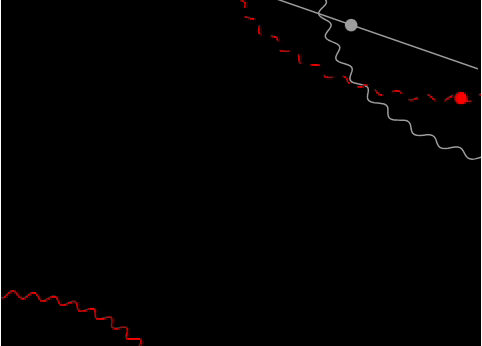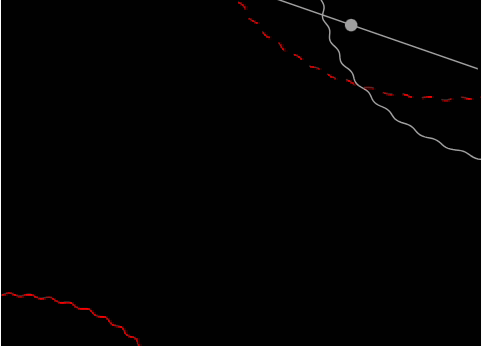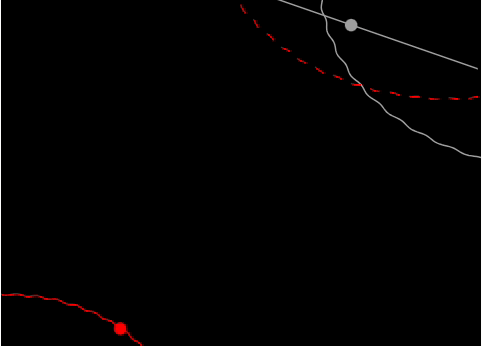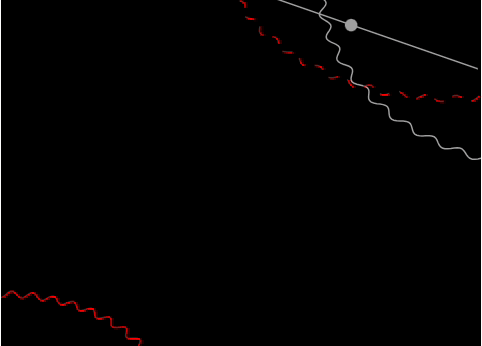
You can experiment with the interval and the TransitionDuration option of Graphics for smoother animation.