Billiard

⏱️ One min read

Maintainer

A toy-like example on the real-time collisions resolution using Verlet Integration method

We shall start with the solver function. The algorithm is straightforward and does not require any special symbolic computations, therefore we write it in the procedural CPU-friendly style and compile it:

Download original notebook

ClearAll[balls, compiled, visible, frameTrigger, angle, reset];

compiled = Compile[{
  {p, _Real, 3}
}, Module[{b = p},
    Do[

     (* Verlet Integration *)
     b[[3]] = b[[2]];
     b[[2]] = b[[1]];
     b[[1]] = 2 b[[2]] - b[[3]];

     (* Particle-particle collisions *)
     Do[
      Do[
        If[i < j,
          Module[{pi = b[[1, i]], pj = b[[1, j]], d, dist, n, overlap},
            d = pj - pi;
            dist = Norm[d];
            If[dist < 0.1, (* Effective Radius *)
              n = Normalize[d];
              overlap = 0.1 - dist;
              b[[1, i]] -= 0.5 overlap n;
              b[[1, j]] += 0.5 overlap n;
            ];
          ]
        ],
        {j, Length[b[[1]]]}
      ],
      {i, Length[b[[1]]]}
     ];   
     , {3}];

     b
  ], "RuntimeOptions" -> "Speed"];

Now we can model our scene. We define a group of stationary balls and then add the last one with a predefined velocity directed towards the center.

balls = Module[{s = 
  With[{r=0.04}, {d=2r}, Flatten[
   Table[
     {d i, (j - i/2) d (*SqB[*)Sqrt[3](*]SqB*)},  
     {i, 0, 8},                   
     {j, 0, i}                     
   ],
   1
  ]]
}, 
    s = Append[s, {0,0}];
    {s,s,s}
];

balls[[1, -1]] = {-2,0};
balls[[2, -1]] = {-2.05,0};
balls[[3, -1]] = {-2,0};

visible = balls[[1]];

frameTrigger = CreateUUID[];

EventHandler[frameTrigger, Function[Null,
    balls = compiled[balls];
    visible = balls[[1]];
]];

Graphics[{
    PointSize[0.03],
    Pink, Point[visible // Offload],
    AnimationFrameListener[visible // Offload, "Event"->frameTrigger]
  }
, PlotRange->3{{-1,1}, {-1,1}}, 
  AspectRatio->1, ImageSize->Medium, 
  TransitionType->None, Frame->True
]

(*VB[*)(Graphics[{PointSize[0.03], RGBColor[1, 0.5, 0.5], Point[Offload[visible]], AnimationFrameListener[Offload[visible], "Event" -> "2f74359b-b819-4e37-9839-8f69c40bfb0d"]}, PlotRange -> {{-3, 3}, {-3, 3}}, AspectRatio -> 1, ImageSize -> Medium, TransitionType -> None, Frame -> True])(*,*)(*"1:eJyNUctKxDAUrTq+EFy6FAS3hdFWp10NKjoKPjv9gaS9GS+kSUnagXHvb/gd8znu/QapSUrFGQTN4nCf5957ckBlwlY8z9M9A9eS52zDelsGRoqUz5hp1uvyt6irtnrbwKNEUY3xBdR8//Xjaf42ZGtdbzI6v5BcKrTVynPvffhttCTrHUnrbhp4YIxLkjt7ihopB7Zqk3sGzgQWpEIprhQpwC4DAtQ/mu3uSc1hbCdeTsGsfWisYzYIg5OY+jQ6iv0QgoEfR0HsR+w0zsI+ZbSfLxK0d3NZJURMfpA7YRY8/GyaBq0ef8cd8449UJeQGW5zoxPul+E3BZmAFV3bf7qDHOtiqWzXGKkiQqPVKp2V4HL3UizJ4T7AaelCqarhC+Tifi4="*)(*]VB*)

Adding Interactivity

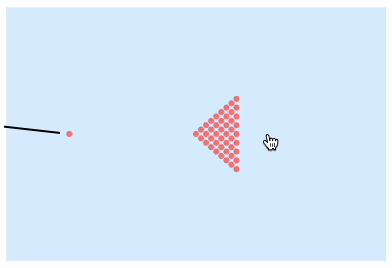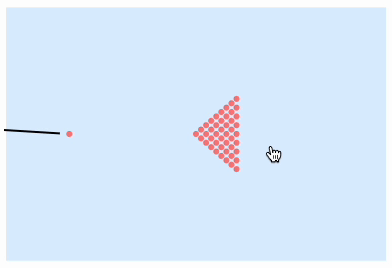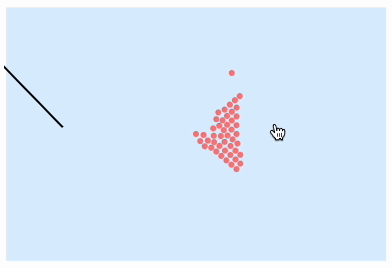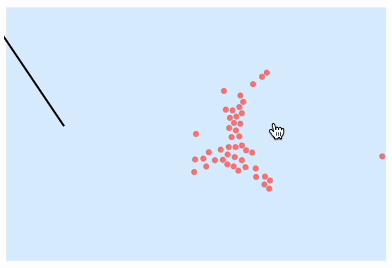
We can give the user an opportunity to knock the ball themselves. For this, we need to track the mouse position and adjust the angle accordingly. And let's add the boundaries as well

reset := balls = Module[{s = 
  With[{r=0.04}, {d=2r}, Flatten[
   Table[
     {d i, (j - i/2) d (*SqB[*)Sqrt[3](*]SqB*)},  
     {i, 0, 8},                   
     {j, 0, i}                     
   ],
   1
  ]]
}, 
    s = Append[s, {-2,0}];
    {s,s,s}
];

reset;

angle = 0.;
visible = balls[[1]];

frameTrigger = CreateUUID[];

EventHandler[frameTrigger, Function[Null,
    balls = compiled[balls];
    balls[[1]] = Map[{Clip[#[[1]], {-3,3}], Clip[#[[2]], {-2,2}]}&, balls[[1]]];
    visible = balls[[1]];
]];

Labeled[EventHandler[Graphics[{
    LightBlue, Rectangle[{-3,-2},{3,2}], PointSize[0.03],
    Pink, Point[visible // Offload],
    Black, AbsoluteThickness[2], 
    Line[With[{x = {Sin[angle], Cos[angle]}}, {-3x + {-2,0}, -0.15 x + {-2,0}}]//Offload],
    AnimationFrameListener[visible // Offload, "Event"->frameTrigger]
  }
, PlotRange->3{{-1,1}, {-1,1}}, 
  AspectRatio->1, ImageSize->Medium,
  ImagePadding->10,
  TransitionType->None, Controls->False
], {
  "mousemove" -> Function[xy, angle = VectorAngle[(xy-balls[[-1,-1]]), {0,1}] // N], 
  "click" -> Function[Null, 
    balls[[1,-1]] += 0.03 {2.85` Sin[angle],2.85` Cos[angle]};
  ]
}], Button["Reset", reset]]

Adding Interactivity​

Adding Interactivity