Basic Verlet Integration implementation

· 4 min read

Kirill Vasin

Maintainer

Using the power of Newton's equations and numerics to solve dynamics of arbitary planar meshes in real-time

Bunch of points

Define a set of random points

Download original notebook

pts0 = RandomReal[{-1,1}, {10, 2}];
pts1 = pts0; pts2 = pts0;

Graphics[{Rectangle[{-10,-10}, {10,10}], Red, Point[pts0 // Offload]}, "Controls"->False]

(*VB[*)(Graphics[{Rectangle[{-10, -10}, {10, 10}], RGBColor[1, 0, 0], Point[Offload[pts0]]}, "Controls" -> False])(*,*)(*"1:eJxdjlsKAjEMResLH7twB67BAccPQakrqDOtBkIzNHXr/ta0pQj+HHLzuLn7B2k3U0rxUnAmHN08q42gD2Z6wcBu0eYX4FjnW4G2QzT+iba22gJ8UkoFf/2dFAXVML/Q/bEjpAA5AqiGmmgluBH4WOVacHUOyYzFc4p8+H3Qb7T3bNmRj4GQy/nJINsvH7wzTQ=="*)(*]VB*)

The Størmer–Verlet method is a variant of the discretization of Newton's equations of motion:

x_{i+1} = 2x_i - x_{i-1} + a_i\, \delta t^2

This method only requires storing the current position $x_{i+1}$ and the two previous positions $x_i$ and $x_{i-1}$ ; velocity is not needed. Try to run this cell below

With[{\[Delta]t = 0.5},
  pts0  = 2 pts1 - pts2 + Table[{0,-1}, {Length[pts0]}] (*SpB[*)Power[\[Delta]t(*|*),(*|*)2](*]SpB*);
  pts2 = pts1;
  pts1 = pts0;
]

We can add random connections to our points (forming bonds) using graphs

bonds = RandomGraph[Length[pts0]{1, 2}, VertexCoordinates->pts0]

(*VB[*)(Graph[{1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, {Null, SparseArray[Automatic, {10, 10}, 0, {1, {{0, 5, 9, 13, 18, 22, 22, 27, 31, 34, 40}, {{2}, {4}, {5}, {8}, {10}, {1}, {4}, {9}, {10}, {4}, {8}, {9}, {10}, {1}, {2}, {3}, {5}, {7}, {1}, {4}, {7}, {10}, {4}, {5}, {8}, {9}, {10}, {1}, {3}, {7}, {10}, {2}, {3}, {7}, {1}, {2}, {3}, {5}, {7}, {8}}}, Pattern}]}, {VertexCoordinates -> {{0.6097071079842546, 0.5710193798306946}, {0.4947448371382195, 0.03477815591969424}, {-0.4796507057494588, 0.04473276586757047}, {-0.34030553279374187, -0.8852674833737066}, {0.1649401002552966, -0.24559529545285486}, {-0.8468460711918513, -0.7206445114959674}, {0.716511927090667, 0.7961901483219602}, {0.8287698960754502, 0.26045296296986464}, {-0.9624145652706186, -0.8017079325257308}, {0.9342990378264822, 0.7007185855469098}}}])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KWlMIB4HkHAvSizIyEwuhojwI4k45+cW5KRWpIIkuIAYRG84LVu9o+mxvYOmRf4p10f2Gc+v2z9bed+eYf4Ul8JzC+1XzF9zf8ame/sdPr/uMXu+zL7iXP3tCcev7k9Zo1kpE/Jmf8E8oxsHZY7aN+xnWrkq//z+OdUT3sVIvt6/IUJWpJX/+X6JnoPZq94+szcQ4zucXPXS3mXrx0KP1lf2DK1tz51WX7D/wJC4UPLMu/0dnU9Spi9/uX/NkRaJ40/f2nd8Ek7yzHlmD/EFyJc+mcUlacyYPE4g4ZJZlJpcklmWCgkUdiDhX5CYnFlSWZQGBkCDwIpBhEdpapExGDy2h0sj1MFNcE4scMsvyg1mBbKD8kvzUiBSoJBzLCrKL89ITUwpLmKAAkR0gJ0GdjYrTGmaCKYkjOcJ0mgIJo1wypjglDHFKWOBVQYkZmiARcoIp0UQGUusMjiNM8ZpnDFO1xnjtMgYt0UmOIMBImOORcYUjwxOi8xxutscp7vNcRtnAZUquqG5zjDAa5p9GjdmIkFN3NiTMCT9PYAxPkCTMKgscE1JTwWlYWyGMcKEgMVDpU9qWWpOJiIdY81BcD+4ZBZnZ4LUIdyOKseER44ZjxwLHjlWPHJseOTY8chx4JHjxCPHhSLHihlvIF5QaU4quLQAxUBiSUhlQSq4OA4pSkzJLMnMz0vMQcQNqoaixNzUkMzk7GKwuF9+XiqaKh4gwzM3MT01IDElJTMvHZc6Tpi64Myq1MwToPhFURAMCgHn/LySovycYnB55ZaYU5wKABn+emI="*)(*]VB*)

The **Størmer–Verlet method** really shines when it comes to solving equations with constraints. In our case, we want to keep the distances between points fixed according to a connection graph. Normally, this would involve approximating motion using a combination of acceleration, velocity, and position. However, things can become complicated quickly. With the Størmer–Verlet method, we only work with positions $ x_i $. By directly adjusting the positions of two points connected by a bond to maintain the bond length, we effectively account for all forces in a single step.

The stiffness of the bond is not directly in the differential equation It’s introduced through how you enforce the constraint — either strictly (hard) or partially (soft). Let's define the initial length $L=|\mathbf{d}|$

\mathbf{d} := \mathbf{x}_a - \mathbf{x}_b

To enforce the bond we compute the correction vector

\Delta \mathbf{d} := \mathbf{d} \cdot k \Big( \frac{L}{|\mathbf{d}| } - 1 \Big)

and then apply it to each point

\begin{align*} \mathbf{x}_a &= \mathbf{x}_a + \frac{1}{2} \Delta \mathbf{d} \\ \mathbf{x}_b &= \mathbf{x}_b - \frac{1}{2} \Delta \mathbf{d} \\ \end{align*}

where $k$ is a stiffness parameter. There are two cases:

$k=1$ hard bond
$k < 1$ soft bond (kinda bouncy like a spring)

Let's try to implement this in pure functions

getDir[bonds_, pts_] := Map[(pts[[#[[1]]]] - pts[[#[[2]]]]) &, bonds] 

applyBond[pairs_, k_:1.0, maxDelta_:0.1][p_] := Module[{pts = p},
  MapThread[Function[{edge, length}, With[{
    diff = pts[[edge[[1]]]] - pts[[edge[[2]]]]
  },
    With[{
      delta =Min[k ( (*FB[*)((length)(*,*)/(*,*)(Norm[diff]+0.001))(*]FB*) - 1), maxDelta] diff
    },
      pts[[edge[[1]]]] += delta/2.0;
      pts[[edge[[2]]]] -= delta/2.0;
    ]
  ] ], RandomSample[pairs]//Transpose];

  pts
] 

Here is a helper function to draw bonds, keeping them coupled to a dynamic symbol so that we can see how they change in real time.

showGeometry[points_, bonds_, opts___] := Graphics[{
  Gray, Rectangle[5{-1,-1}, 5{1,1}], Blue,
  
  Table[
    With[{i = edge[[1]], j = edge[[2]]},
      Line[With[{
        p = points
      }, {p[[i]], p[[j]]}]] // Offload
    ]
  , {edge, bonds}],
  
  Red, Point[points // Offload]
}, opts]

SetAttributes[showGeometry, HoldFirst];

Show it using our randomly generated points

showGeometry[pts0, EdgeList @ bonds]

(*VB[*)(FrontEndRef["a5b31a9d-b6d6-4c3e-b884-a85c8357c438"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKJ5omGRsmWqboJpmlmOmaJBun6iZZWJjoJlqYJlsYm5onmxhbAACMnhWu"*)(*]VB*)

We are almost set for our animation! Let's regenerate random points and connections each time we evaluate the next cell and run the main update loop, which consists of Verlet methods combined with hard constraints

pts0 = RandomReal[{-1,1}, {10, 2}];
pts1 = pts0; pts2 = pts0;

bonds = EdgeList[RandomGraph[Length[pts0]{1, 3}]];
lengths = Norm /@ getDir[bonds, pts0];
pairs = {bonds, lengths} // Transpose;

Do[With[{\[Delta]t = 0.05},
  pts0 = Clip[applyBond[pairs, 1.0][
    2 pts1 - pts2 + Table[{0,-1}, {i, Length[pts0]}] (*SpB[*)Power[\[Delta]t(*|*),(*|*)2](*]SpB*)
  ], {-5,5}];
  
  pts2 = pts1;
  pts1 = pts0;
  
  Pause[0.01];
  
], {i, 200}]

Procedurally generated structures

Even without any optimizations of present code (normally you would need to use vectorization tricks or Compile or switch to OpenCLLink) we can still try to model some more complex than random graph of 10 points and add interaction with a user's mouse.

Rim

Here is a quick way of making this using just tables

rim = Join @@
  (Table[#{Sin[x], Cos[x]}, {x,-Pi, Pi, Pi/6}] &/@ {1, 0.9} // Transpose);
  
rbonds = Graph[
  Join[
    Table[i<->i+1, {i, 1, Length[rim]-1}],
    Table[i<->i+2, {i, 1, Length[rim]-2, 2 }],
    Table[i<->i+2, {i, 2, Length[rim]-4, 2 }],
    {Length[rim]-2 <-> 2},
    {Length[rim]-1 <-> 1}
  ]
, VertexCoordinates->rim]

rbonds = EdgeList[rbonds];
rpairs = {rbonds, Norm /@ getDir[rbonds, 2.0 rim]} // Transpose;

(*VB[*)(CoffeeLiqueur`Extensions`Boxes`Workarounds`temporal$555644)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKJ1kaGiZZmBnpWpgYG+qaANm6FqmmhrqJBsmJSWZGyUmJZmYAd84VZQ=="*)(*]VB*)

Prepare variables for storing positions

rim0 = 2.0 rim; rim1 = rim0; rim2 = rim0;
rimR = rim0;

mousePos   = {100.,0.};

Here we will automate our update cycle by attaching an animation frame listener to the rimR symbol. It will trigger an event to prepare the next frame of animation within the update cycle of your screen (actually - the app window). Each time, the timer is reset by an update of the rimR symbol, ensuring that the next frame will only come after the previous one has been finished.

EventHandler[
  showGeometry[rimR, rbonds, TransitionType->None, "Controls"->False, Epilog->{
    AnimationFrameListener[rimR // Offload, "Event"->"anim"], 
    Circle[mousePos // Offload, 0.5]
  }, PlotRange->{{-5,5}, {-5,5}}]
, {"mousemove" -> Function[xy,
    mousePos = xy;
]}]

(*VB[*)(FrontEndRef["3bce9eb6-f53f-4ddb-8443-f7d28a8076ec"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKGyclp1qmJpnpppkap+mapKQk6VqYmBjrppmnGFkkWhiYm6UmAwCVvhZE"*)(*]VB*)

Animation controls

Button["Start", 
 EventHandler["anim", With[{}, Do[With[{\[Delta]t = 0.006}, 
  rim0 = applyBond[rpairs, 1.0, 0.8][
    Clip[(2 rim1 - rim2) + Table[
       If[Max[Abs[i - mousePos]] < 2.0, {0,-1} - 7.0 (i - mousePos), {0,-1}]
    , {i, rim0}] (*SpB[*)Power[\[Delta]t(*|*),(*|*)2](*]SpB*), {-5,5}]
  ];

  
  rim2 = rim1;
  rim1 = rim0;
  
 ], {i, 10}];
  rimR = rim0;

 ]&]; 
 rimR = rim0;
]

Button["Stop", EventRemove["anim"]]

Button["Reset", With[{}, rim0 = 2.0 rim; rim1 = rim0; rim2 = rim0;
rimR = rim0;]]

Generate a Mesh from an Image

The more challenging, the more fun! It would be great to sketch a bitmap image using a brush and transform it into a mesh that can be modeled.

mask = NotebookStore["carnivorous-284"];
EventHandler[InputRaster[mask], (mask = #)&]

(*VB[*)(EventObject[<|"Id" -> "c55c1db7-d2bc-405f-92b2-ff686e34700f", "View" -> "071dc109-8cda-4156-8af8-c541963477de"|>])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKG5gbpiQbGljqWiSnJOqaGJqa6VokplnoJpuaGFqaGZuYm6ekAgB91BVN"*)(*]VB*)

Now convert this image to a mesh, triangulate it and render as an index graph. Using Graph object is a bit easier, than working with triangulated mesh, since all bonds are sorted and can easily be extracted

mesh = TriangulateMesh[
  ImageMesh[ImageResize[mask , 100]// ColorNegate]
, MaxCellMeasure->{"Area"->100}];

graph = MeshConnectivityGraph[mesh, 0] // IndexGraph
vertices = graph // GraphEmbedding;
edges = (List @@ #) &/@ (graph // EdgeList) (*BB[*)(*convert to list of lists*)(*,*)(*"1:eJxTTMoPSmNhYGAo5gcSAUX5ZZkpqSn+BSWZ+XnFaYwgCS4g4Zyfm5uaV+KUXxEMUqxsbm6exgSSBPGCSnNSg9mAjOCSosy8dLBYSFFpKpoKkDkeqYkpEFXBILO1sCgJSczMQVYCAOFrJEU="*)(*]BB*);

vertices = Map[Function[x, x - {0.4,-1.2}], 0.04 vertices] (*BB[*)(*scale and translate*)(*,*)(*"1:eJxTTMoPSmNhYGAo5gcSAUX5ZZkpqSn+BSWZ+XnFaYwgCS4g4Zyfm5uaV+KUXxEMUqxsbm6exgSSBPGCSnNSg9mAjOCSosy8dLBYSFFpKpoKkDkeqYkpEFXBILO1sCgJSczMQVYCAOFrJEU="*)(*]BB*);

(*VB[*)(CoffeeLiqueur`Extensions`Boxes`Workarounds`temporal$824230)(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKJ6ampBlbpFnompknmuqaGBsa6VqaJVvqmpuaGyWnGFokGacYAQCH7xWE"*)(*]VB*)

Animation cycle (as before)

vertices0 =  vertices; vertices1 = vertices0; vertices2 = vertices0;
verticesR = vertices0;

vpairs = {edges, Norm /@ getDir[edges, vertices0]} // Transpose;

mousePos   = {100.,0.};

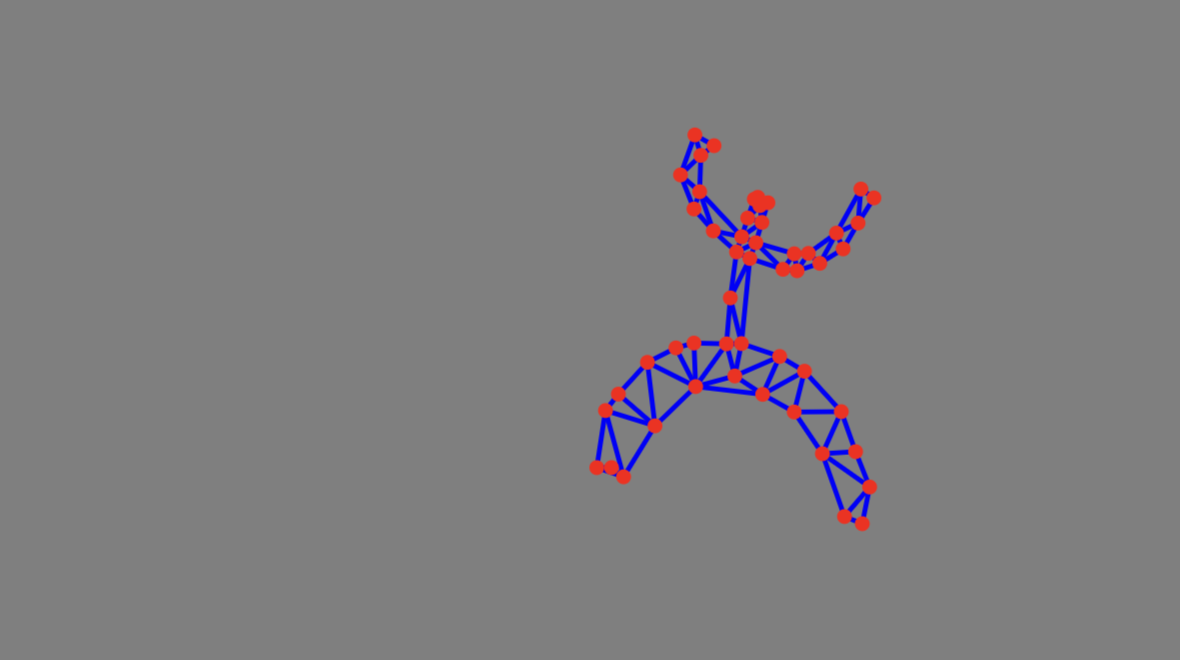
EventHandler[
  showGeometry[verticesR, edges, TransitionType->None, "Controls"->False, Epilog->{
    AnimationFrameListener[verticesR // Offload, "Event"->"anim2"], 
    Circle[mousePos // Offload, 0.5]
  }, PlotRange->{{-5,5}, {-5,5}}]
, {"mousemove" -> Function[xy,
    mousePos = xy;
]}]

(*VB[*)(FrontEndRef["042dbb94-164f-4875-860c-7e260c54bedb"])(*,*)(*"1:eJxTTMoPSmNkYGAoZgESHvk5KRCeEJBwK8rPK3HNS3GtSE0uLUlMykkNVgEKG5gYpSQlWZroGpqZpOmaWJib6lqYGSTrmqcaASlTk6TUlCQAecUVdQ=="*)(*]VB*)

Button["Start", 
 EventHandler["anim2", With[{}, Do[With[{\[Delta]t = 0.003}, 
  vertices0 = applyBond[vpairs, 1.0, 0.8][
    Clip[(2 vertices1 - vertices2) + Table[
       If[Max[Abs[i - mousePos]] < 2.0, {0,-1} - 7.0 (i - mousePos), {0,-1}]
    , {i, vertices0}] (*SpB[*)Power[\[Delta]t(*|*),(*|*)2](*]SpB*), {-5,5}]
  ];

  
  vertices2 = vertices1;
  vertices1 = vertices0;
  
 ], {i, 3}];
  verticesR = vertices0;

 ]&]; 
 verticesR = vertices0;
]

Button["Stop", EventRemove["anim2"]]

Button["Reset", With[{}, vertices0 =  vertices; vertices1 = vertices0; vertices2 = vertices0;
verticesR = vertices0;]]

As a next step I would suggest to you take Compile expression and try keep all pure functions there. Thank you fro your attention 🧙🏼‍♂️

Bunch of points​

Procedurally generated structures​

Rim​

Generate a Mesh from an Image​

Bunch of points

Procedurally generated structures

Rim

Generate a Mesh from an Image